By Paul Roggemans and Peter Cambell-Burns
An independent search among 685362 public available orbits showed the presence of a concentration of similar orbits for both the Zeta Cygnids (ZCY) and April Rho Cygnids (ARC). The resulting orbital elements for the two showers confirm a small difference in inclination and argument of perihelion but this does not exclude a common origin. There is no sign of any periodicity and the ARC filament was not in outburst in 2012. The Nu-Cygnids (NCY-409) entry in the IAU working list of meteor showers is identical to the April Rho-Cygnids (ARC–348). The radiant drift corrected positions have a large overlap. The shower characteristics are identical. The activity profiles display several sub-maxima and suggest a layered structure of superimposed streamlets left over from a single parent body, either a Halley type comet or Jupiter family comet.
1 Introduction
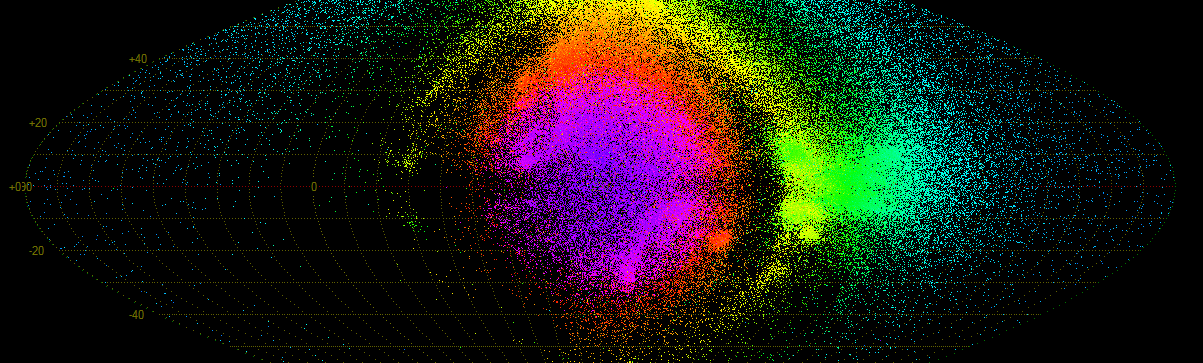
Looking for the ζ-Cygnids on the CAMS website we find the radiants of these orbits spread over a large region of the sky, almost the entire constellation of Cygnus (Figure 1). A widely scattered radiant area is typical for an old diffuse meteor stream. Checking the individual radiant points, we see that some radiants are identified as April ρ-Cygnids (ARC–348) although the geocentric velocity is about the same as for the ζ-Cygnids (ZCY–040). To make the picture complete, the IAU working list of meteor showers also mentions a third unconfirmed shower, the ν-Cygnids (NCY–409) in the same time lapse in the same radiant area but without any orbital elements. The naming of a meteor shower according to the star near the center of the shower radiant can be misleading in the sense that this creates a false impression of accuracy. Most shower radiant sizes are poorly known and the median value for the radiant position differs by several degrees for different datasets. Meteor showers have a complex and dynamic nature while the observational accuracy in orbit determination tend to be overestimated, leading to too optimistic interpretations.
Although the initial idea for this paper was a case study on the ζ-Cygnids, the preliminary verifications of the available orbit data indicated a more complex picture. The presence of at least one established meteor shower at about the same radiant position in the same time span with almost identical velocity and characteristics required a wider scope to review these showers. Although two showers of different origin may share the same radiant area with an overlap in activity period, it looks more appropriate to consider the April–May Cygnid radiants as a single complex with different streamlets that were detected and listed as separate showers. The small differences in orbital elements for the different filaments could be explained as the result of planetary perturbations by nearby planet Jupiter, something that remains to be proven by stream modelers. Figure 1 also shows the Lyrid radiant, a much more compact radiant.

Figure 1 – Screenshot of the CAMS radiant plot for the night of 2018 April 22 with the widely scattered radiants identified as Zeta Cygnids (040). Some of the green dots are identified as April Rho Cygnids (348).
2 ZCY (040) and ARC (348) history
Attempts to find similar orbits in the photographic meteor orbit catalogue with 4873 accurate photographic orbits obtained between 1936 and 2008 were negative. The Harvard radar orbit catalogues 1961–1965 and 1968–1969 (Hawkins, 1963) contain several orbits with a low threshold of DD < 0.105 for both reference orbits. The first mention in literature of the ζ-Cygnids appeared in a stream search on radio orbits (Sekanina, 1976).
A radiant search on single station video meteors (Molau and Rendtel, 2009) listed 402 meteors identified as ζ-Cygnids but with an activity period and maximum well ahead of the period determined in later shower searches based on video orbits. This detection might be spurious as it is based on backwards projection of single station meteor paths and not on orbital data. This radiant search also revealed the ν-Cygnids (NCY–409) based on 508 single station meteor trails, included in the IAU working list of meteor showers although no reference orbit is available for this type of data. The proximity of the very active Lyrids (LYR–006) near its maximum activity combined with the natural sporadic background activity may seriously distort any attempts to derive minor shower radiants from single station video data. The activity period and time of best activity correspond to the shower component for the ζ-Cygnids obtained from our analyses.
The April ρ-Cygnids (ARC–348) were discovered by CMOR from orbit data collected 2002–2009 (Brown et al., 2010) while the ζ-Cygnids (ZCY–040) shower was not detected in this search. The analysis by Brown et al. (2010) also suggests a possible association between the ARC–348 shower and the May Lacertids (MAL–350).
Phillips et al. (2011) confirmed the activity of the ARC shower with 29 CAMS orbits obtained between April 27 and May 7 with low activity peaks on April 28 and May 1. Clear weather in 2012 between April 15 and 23 allowed CAMS to collect 1362 orbits (Jenniskens and Halberman, 2013). Based on this dataset evidence was found for the ν-Cygnids (NCY–409) for which IMO claimed discovery in 2009. The authors concluded that the NCY was not another manifestation of the nearby April ρ-Cygnids as the radiant position in the 2012 CAMS dataset was separated in time and position. Because the shower did not appear in the meteor stream search of SonotaCo the question arose whether this shower was in “outburst” in 2012 although only very small numbers of similar orbits were collected.
In a later study Jenniskens et al. (2016) concluded that the NCY–409 discovery was identical to the ζ-Cygnids (ZCY–040) and should be removed from the working list. However, at the time of writing this paper the NCY–409 entry remains the list. All the reference orbits listed in the IAU working list of meteor showers are listed in Table 4.
3 The available orbit data
We have the following data, status as of June 2018, available for our search:
- EDMOND EU+world with 317830 orbits (until 2016). EDMOND collects data from different European networks which altogether operate 311 cameras (Kornos et al., 2014).
- SonotaCo with 257010 orbits (2007–2017). SonotaCo is an amateur video network with over 100 cameras in Japan (SonotaCo, 2009).
- CAMS with 110521 orbits (October 2010 – March 2013), (Jenniskens et al., 2011). For clarity, the CAMS BeNeLux orbits April 2013 – May 2018 are not included in this dataset because this data is still under embargo.
Altogether we can search among 685362 video meteor orbits.
4 Orbit selection
Although we have reference orbits from previous research, we want to check if we can find any evidence for the existence of this shower. If some concentration of similar orbits can be found, we can try to calculate our own reference orbit.
In a previous series of shower analyses (Roggemans and Johannink, 2018; Roggemans, 2018; Roggemans and Campbell-Burns, 2018a, 2018b, 2018c, 2018d) we selected a time span in solar longitude around the time of maximum. Without any idea about the activity period, this required some steps to extend the time span until no more similar orbits were found. To have a better idea of the activity period and spread of the radiant positions, we compiled a single list of the 685362 orbits to make a preliminary selection using the reference orbit from literature and the D-criteria of Southworth and Hawkins (1963), Drummond (1981) and Jopek (1993). We considered four different threshold levels of similarity:
- Low: DSH < 0.25 & DD < 0.105 & DH < 0.25;
- Medium low: DSH < 0.2 & DD < 0.08 & DH < 0.2;
- Medium high: DSH < 0.15 & DD < 0.06 & DH < 0.15;
- High: DSH < 0.1 & DD < 0.04 & DH < 0.1.
Next, we derived the minima and maxima for the solar longitude, right ascension, declination and geocentric velocity for the orbits that fulfill the low threshold D-criteria. These limits were used to extract the selection of orbits used for this analysis. We applied this procedure to make two selections, one for the ζ-Cygnids (ZCY–040) and one for the April ρ-Cygnids (ARC–348).
For the case of the ζ-Cygnids this procedure resulted in the following selection with 969 orbits:
- Time interval: 17° < λʘ < 46°;
- Radiant area: 294° < α < 325° & +33° < δ < +52°;
- Velocity: 36 km/s < vg < 49 km/s.
For the case of the April ρ-Cygnids this procedure resulted in the following selection with 618 orbits:
- Time interval: 25° < λʘ < 52°;
- Radiant area: 307° < α < 338° & +38° < δ < +56°;
- Velocity: 35 km/s < vg < 47 km/s.
The individual radiant positions for both showers appeared mixed in the large radiant region with the eastern part of the large radiant mainly populated by ARC-radiants while the ZCY-radiants dominated in the western part. In total we got 1143 different orbits for both ARC and ZCY selections together of which 444 orbits appear in common in both selections.
5 Shower case study
The median values of each selection were used as parent orbit to calculate D-criteria in a first approach to find the orbits with a similarity which indicates a dust concentration. The median values obtained for the orbits which fulfill the high threshold level are taken as a new parent orbit to recalculate the D-criteria to obtain the final median values for the different threshold levels. The final results for the above-mentioned threshold levels are listed in Table 1 for the ζ-Cygnids selection and in Table 2 for the April ρ-Cygnids.
The differences between both showers are very small; The April ρ-Cygnids have a reference orbit about 6° in solar longitude later than the ζ-Cygnids, a slight lower velocity and lower inclination. Particles of both showers share to a large extend the same space in the solar system, with many orbits that fulfil the D-criteria for both parent orbits. The question arises on which criteria these two showers were identified as two physically separated meteor streams? The similarity between the two datasets with orbits suggests that both are dust trails within a single diffuse meteor stream complex.
Table 1 – The median values for the final selected orbits with four different threshold levels on the D-criteria, compared to the reference orbit from literature for the ζ-Cygnids (Jenniskens et al., 2016).
| Low | Medium low | Medium high | High | Reference (2016) | |
| λʘ | 31.4° | 31.9° | 31.9° | 33.2° | 32.0° |
| αg | 310.3° | 311.4° | 311.3° | 311.7° | 309.5° |
| δg | +43.5° | +43.7° | +43.5° | +44.4° | +42.5° |
| vg | 42.6 | 42.7 | 44.4 | 44.1 | 43.0 |
| a | 5.2 | 5.1 | 5.1 | 5.2 | 3.93 |
| q | 0.892 | 0.888 | 0.892 | 0.898 | 0.900 |
| e | 0.830 | 0.827 | 0.821 | 0.826 | 0.780 |
| ω | 138.7° | 138.1° | 138.5° | 139.5° | 140.5° |
| Ω | 31.4° | 31.9° | 31.9° | 33.2° | 31.5° |
| i | 73.5° | 73.7° | 74.0° | 73.3° | 74.9° |
| N | 405 | 185 | 77 | 20 | 64 |
| S | 58% | 81% | 92% | 98% |
Table 2 – The median values for the selected orbits with four different threshold levels on the D-criteria, compared to the reference orbit from literature for the April ρ-Cygnids (Jenniskens et al., 2016).
| Low | Medium low | Medium high | High | Reference (2016) | |
| λʘ | 35.8° | 37.2° | 38.5° | 40.3° | 38.0° |
| αg | 320.0° | 321.4° | 322.4° | 324.7° | 322.1° |
| δg | +46.6° | +46.6° | +47.4° | +48.4° | +46.6° |
| vg | 41.4 | 41.3 | 41.0 | 40.9 | 40.9 |
| a | 6.0 | 6.1 | 5.9 | 6.4 | 6.14 |
| q | 0.852 | 0.847 | 0.842 | 0.833 | 0.842 |
| e | 0.860 | 0.858 | 0.856 | 0.870 | 0.864 |
| ω | 132.0° | 131.2° | 130.3° | 128.8° | 130.3° |
| Ω | 35.8° | 37.2° | 38.5° | 40.3° | 39.4° |
| i | 69.6° | 69.6° | 68.9° | 68.6° | 69.7° |
| N | 346 | 210 | 111 | 32 | 42 |
| S | 44% | 66% | 82% | 95% |
Figure 2 shows the plot of the inclination versus length of perihelion for both ‘showers’. There is a diffuse but distinct concentration of similar orbits. The large overlap in space for the orbits of the two components becomes obvious in this plot, with a slight difference of 3° in length of perihelion and about 5° in inclination. It is impossible to distinguish the orbit association properly for many orbits with these two parent orbits. For this reason, we combine the case study for both showers to see if we find more indications that both showers are in fact diffuse dust trails of a single shower complex.
 |
 |
| Figure 2 – The plot of inclination i (°) against the length of perihelion П (°) for the 969 preselected possible ZCY-orbits at left and for the 618 ARC-orbits at right. The colors mark the different threshold levels of the D-criteria listed in Table 1 and Table 2, the yellow triangles mark the final reference orbits. | |
There is no indication for any periodicity in the annual activity. Orbits for both shower components are registered during each year. The variation from year to year can be perfectly explained as statistical fluctuations. The question if the NCY–409, later considered as another instance of the ARC–348 shower, were in outburst in 2012 can be answered by this study. There was annual activity and no sign of any outburst. The fact that the shower did not occur in the meteor stream search of SonotaCo orbits 2007–2011, does not prove that SonotaCo did not contain orbits of the ARC shower. Our analyzes include 26 possible ARC orbits for SonotaCo for 2007–2011.

Figure 3 – The percentage of ZCY orbits per year (DD < 0.105) relative to the total number of orbits obtained that year during the ZCY activity period.

Figure 4 – The percentage of ARC orbits per year (DD < 0.105) relative to the total number of orbits obtained that year during the ARC activity period.
The activity of minor showers such as the ZCY and ARC showers remains far below the statistical limits required to obtain any zenithal hourly rates or flux rates. Instead, we can make a simple estimate of the activity profile by counting the number of orbits accumulated per degree of solar longitude during a significant time span, e.g. 10 years or more, compensating years with unfavorable circumstances. This approach ignores all influences that may affect hourly rates and therefore it is not the ideal way to proceed, but given the long period of time and the large global scale to collect orbits, this approach will give a good idea of the number of shower orbits encountered by the Earth per solar longitude.
Figure 5 shows the number of orbits per degree of solar longitude for both showers for the different threshold levels of the D-criteria. For the low threshold level, the two showers together count 529 orbits of which 223 orbits fulfil the criteria for both parent orbits. These 223 orbits appear in both activity profiles what explains the common parts in the profile. The first peak in Figure 5 (left) at λʘ = 31.5° and a second peak at λʘ = 33.5° are due to the
ζ-Cygnids. A third peak at λʘ = 38.5° in the ζ-Cygnids profile is due to April ρ-Cygnids that fulfil the D criteria for the parent orbit of the ζ-Cygnids. The first two peaks in Figure 5 (right) with the activity profile for the April
ρ-Cygnids is due to ZCY-orbits that fulfil the D-criteria for the parent orbit of the April ρ-Cygnids. The peak at λʘ = 38.5° (~April 29) corresponds to the time of maximum activity given in Table 2 (Jenniskens et al., 2016). Figure 5 seems to show a secondary peak two days later at λʘ = 40.5° (May 1), which may correspond to the second of two peaks reported in 2011 by Phillips et al. (2011). Considered as one single stream the ZCY and ARC activity looks like a layered structured with successive filaments of dust concentrations comparable to the structure of the Orionid shower in October but at a much lower activity level. The first peaks on the profile in Figure 5 may be associated with the earlier instances of ZCY activity reported by Sekanina (1976) and Jenniskens et al. (2018). The last peak in the ARC profile may be due to the May Lacertids (MAL–350) activity associated with the ARC shower by Brown et al. (2010) (Table 4).
Table 3 – Radiant drift with ± σ for the two shower components obtained from the orbits for each threshold level of the D-criteria.
| Threshold level | ZCY – 040 | ARC – 348 | ||
| Δα / λʘ | Δδ / λʘ | Δα / λʘ | Δδ / λʘ | |
| Low | 0.93±0.03 | 0.28±0.03 | 0.93±0.05 | 0.32±0.03 |
| Medium low | 0.86±0.05 | 0.29±0.05 | 0.98±0.06 | 0.33±0.04 |
| Medium high | 0.82±0.09 | 0.20±0.09 | 1.07±0.07 | 0.31±0.05 |
| High | 1.02±0.21 | 0.32±0.21 | 0.93±0.15 | 0.22±0.14 |
Both shower components allow deriving a radiant drift in Right Ascension and declination with a reasonable result for all four threshold levels (Figures 6 and 7, Table 3). The resulting radiant drift suggests that we have two components of the same meteor shower seen few days apart. The ZCY radiant drift starting from λʘ = 31.5° gets the ZCY radiant close to the ARC radiant position at λʘ = 38.5°. Figure 8 shows how scattered and diffuse the uncorrected radiant positions for both the ZCY and ARC components appear. Applying the radiant drift valid for the medium low threshold we see two changes in the plot: the scatter on the remaining sporadic radiants (black dots) increases while the radiants with possible shower association contracts into a more compact radiant area (Figure 9). This proves that the radiant drift is valid. Both plots also show that the two corrected radiant areas have a lot of overlap when corrected for radiant drift for the 5° in solar longitude difference in time for which the plots are valid.
Another way to have an idea about the size and shape of the radiant area is a plot of the solar centered ecliptic coordinates shown in Figure 10. We can see a rather large sized radiant area. The April ρ-Cygnids picture appears slightly more diffuse than that for the ζ-Cygnids.
The median values for the beginning and ending heights of the ζ-Cygnids are 102.8 ± 4.0 and 91.8 ± 4.1, for the April ρ-Cygnids these values are almost identical with 102.0 ± 4.2 and 91.6 ± 4.5. These ablation heights are well above the average values for a geocentric velocity of ~42 km/s which is an indication for a very volatile composition, typical for meteoroids of a cometary origin.
Both ZCY and ARC components are rich in bright meteors and deficient in faint meteors. The median values that were found for the brightness of the ζ-Cygnids was mabs = –0.6 [–4.8 to +2.5], for the April ρ-Cygnids we got mabs = –0.6 [–5.5 to +2.7]. These characteristics are typical for an older shower which lost its smaller particles with time.
 |
 |
| Figure 5 – The number of ζ-Cygnids orbits (left) and April ρ-Cygnids orbits (right), collected per degree of solar longitude λʘ during the period 2007–2017 with blue for DD < 0.105, green for DD < 0.08, orange for DD < 0.06 and red for DD < 0.04.
|
|
 |
 |
| Figure 6 – Radiant drift in Right Ascension α against solar longitude λʘ, for ζ-Cygnids orbits (left) and April ρ-Cygnids orbits (right). The different colors represent the 4 different levels of similarity.
|
|
 |
 |
| Figure 7 – Radiant drift in declination δ against solar longitude λʘ, for ζ-Cygnids orbits (left) and April ρ-Cygnids orbits (right). The different colors represent the 4 different levels of similarity.
|
|
 |
 |
| Figure 8 – Plot of the radiant positions as selected, for 969 ζ-Cygnids orbits (left) and 618 April ρ-Cygnids orbits (right). The different colors represent the 4 different levels of similarity according to different threshold levels in the D-criteria. The yellow triangles mark the final reference orbits.
|
|
 |
 |
| Figure 9 – Plot of the radiant drift corrected radiant positions, for ζ-Cygnids orbits (left) and April ρ-Cygnids orbits (right). The different colors represent the 4 different levels of similarity. The yellow triangles mark the final reference orbits.
|
|
 |
 |
| Figure 10 – Plot of the ecliptic latitude β against the Sun centered longitude λ – λʘ, for ζ-Cygnids orbits (left) and April ρ-Cygnids orbits (right). The different colors represent the 4 different levels of similarity. The yellow triangles mark the final reference orbits. | |
Table – 4 The orbital data for the ZCY–040, ARC–348, NCY–409 and MAL–350 all J2000.
| λʘ (°) |
αg (°) |
δg (°) |
Δα (°) |
Δδ (°) |
vg km/s |
a AU |
q AU |
e | ω (°) |
Ω (°) |
i (°) |
N | Source |
| 16 | 299.0 | +40.2 | 0.5 | 0.3 | 43.6 | 402 | ZCY Molau & Rendtel (2009) | ||||||
| 20 | 303.8 | +44.8 | 39 | 3.86 | 0.898 | 139.8 | 19.2 | 66.4 | 30 | ZCY Sekanina (1976) | |||
| 21.8 | 301.4 | +40.4 | 42.5 | 3.84 | 0.909 | 0.765 | 142.2 | 21.8 | 74.3 | 87 | ZCY Jenniskens et al. (2018) |
||
| 30.0 | 305.2 | +39.4 | 1.8 | 0.7 | 40.4 | 508 | NCY (IMO) | ||||||
| 31.6 | 309.9 | +41.3 | 43.3 | 3.7 | 0.893 | 137.3 | 31.6 | 74.6 | 37 | NCY Jenniskens (2013) | |||
| 31.9 | 311.4° | +43.7 | 0.86 | 0.29 | 42.7 | 5.1 | 0.888 | 0.827 | 138.1 | 31.9 | 73.7 | 185 | ZCY This study DD<0.08 |
| 32.0 | 309.5 | +42.5 | 0.64 | 0.26 | 43.0 | 3.93 | 0.900 | 0.780 | 140.5 | 31.5 | 74.9 | 64 | ZCY Jenniskens et al. (2016) |
| 37.0 | 324.5 | +45.9 | 0.61 | 0.36 | 41.8 | 6.51 | 0.810 | 0.875 | 125.6 | 37.0 | 69.9 | 1006 | ARC Brown et al (2010) |
| 37.2 | 321.4 | +46.6 | 0.98 | 0.33 | 41.3 | 6.1 | 0.847 | 0.858 | 131.2 | 37.2 | 69.6 | 210 | ARC This study DD<0.08 |
| 38.0 | 322.1 | +46.6 | 0.66 | 0.32 | 40.9 | 6.14 | 0.842 | 0.864 | 130.3 | 39.4 | 69.7 | 42 | ARC Jenniskens et al. (2016) |
| 38.9 | 320.9 | +46.5 | – | – | 41.1 | 4.58 | 0.848 | 0.815 | 131.4 | 38.9 | 70.1 | 252 | ARC Jenniskens et al. (2018) |
| 39.9 | 324.5 | +45.9 | 41.8 | 5.56 | 0.844 | 130.4 | 39.9 | 69.7 | 29 | ARC Phillips et al. (2011) | |||
| 42.0 | 335.6 | +45.3 | 0.61 | 0.5 | 43 | 11.14 | 0.725 | 0.935 | 114.8 | 42.0 | 70.6 | 881 | MAL Brown et al. (2010) |

Figure 11 – Some of the reference orbits listed in Table 4, colors correspond to the following references: ZCY (orange) this study DD<0.08, ZCY (red) Jenniskens et al. (2018), ZCY (green) Jenniskens et al. (2016), ARC (blue) Brown et al. (2010), ARC (purple) this study, ARC (pink) Jenniskens et al. (2016), ARC (grey) Jenniskens et al. (2018), MAL (blue) Brown et al. (2010).

Figure 12 – The 20 ZCY–040 orbits that fulfill the high threshold value (red), the 32 ARC–348 orbits that fulfill the high threshold values (blue).

Figure 13 – The 20 ZCY–040 orbits that filfill the high threshold value (red), the 32 ARC–348 orbits that fulfill the high threshold values (blue), seen in the orbital plane of the stream.
6 Comparing orbits
In Table 4 we list the different orbits as listed in the IAU Working list. The interpretation of this data requires some reflections.
Certain entrees concern shower discoveries for which no orbit is known or for which the orbital elements are incomplete. Defining meteor showers based on single meteor station tracks is based on the 19th century methodology of the visual era which led to a lot of controversy. It makes very little sense to apply this 19th century methodology to the more accurate single station video data when orbit data is available. A minimum criterion for any shower discovery should be a statistical relevant sample of accurate orbits.
Observational errors have still a significant effect on the resulting orbits, also for those reference orbits with ‘accurate’ orbits. Video records allow collecting statistical significant number of orbits, but all these orbits have uncertainty margins caused by observational limitations, also the triangulation solution is a best fit but not exact. Most sensitive is the velocity measurement which seriously affects the semi-major axis a resulting in a huge scatter at the aphelia. The difference between the different reference orbits for both ζ-Cygnids and April ρ-Cygnids is well visible in Figure 11.
Old dispersed meteor streams intersect the Earth orbit over a considerable long period of time which means mainly large differences in both the descending node Ω and the argument of perihelion ω. The D criteria are unsuitable to associate physical related obits that are dispersed greatly. The grouping we see in Figure 12 which corresponds to the ζ-Cygnids (red) and April ρ-Cygnids (blue) may be the result of the preliminary selection of orbits in two different time intervals. Figures 12 and 13 show how the orbits with the highest similarity for each component are weaved in between each other.
Peter Jenniskens et al. (2016) classified the April ρ-Cygnids as a Halley Type Comet shower in the toroidal source, while the ζ-Cygnids are considered as a Jupiter Family Comet shower in the toroidal source, because of a slight lower inclination of the April ρ-Cygnids. The ZCY–040 and ARC–348 are listed as possibly paired showers in the toroidal ring.
The very first mention of this stream appeared in the stream search on radio meteor orbits by Sekanina (1976) and the naming in the original paper was “April Cygnids”, more appropriate than ζ-Cygnids for such scattered radiant. If the shower naming would be reconsidered April-May Cygnids would be a more appropriate naming.
7 Conclusion
The attempt to document the ζ-Cygnids (ZCY–040) shower required to take the probably related April ρ-Cygnids (ARC–348) into account. An independent search among 685362 public available orbits proved evidence for the presence of a concentration of similar orbits for the two selections on (λʘ, αg, δg, vg), for both showers, ZCY and ARC. The resulting orbital elements for the two showers are very similar with the references in literature and differ only within the error margins.
Both sources have orbits every year since 2007, there is no indication for any periodicity. The ARC filament was not in outburst in 2012 as we have plenty of orbits each previous year. The ν-Cygnids (NCY–409) entry in the IAU working list of meteor showers is definitely another entry identical to the April ρ-Cygnids (ARC–348). The radiant drift obtained in this analyzes shows the drift corrected ZCY radiant overlapping to a large extend with the ARC radiant, with median values only few degrees apart within a rather large scattered radiant area. The ablation heights and brightness for both ZCY and ARC meteors are identical, indicating a similar origin. The activity profile shows multiple sub-maxima that may be an indication for a layered structure of superimposed streamlets left over from a single parent body, either a Halley Type comet or Jupiter Family comet. Our results confirm the difference in inclination between the ARC and ZCY components. The activity profile with different sub-maxima can explain the differences in time of maximum activity, radiant position and orbital elements between the different literature sources listed in Table 4. The different sub-maxima caused by different streamlets are likely the remnants of an old diffuse meteor shower of cometary origin.
Acknowledgment
The authors are very grateful to Jakub Koukal for updating the dataset of EDMOND with the most recent data, to SonotaCo Network (Simultaneously Observed Meteor Data Sets SNM2007–SNM2017), to CAMS (2010–2013) and to all camera operators involved in these camera networks.
References
Brown P., Wong D. K., Weryk R. J. and Wiegert P. (2010). “A meteoroid stream survey using the Canadian Meteor Orbit Radar. II: Identification of minor showers using a 3D wavelet transform”. Icarus, 207, 66–81.
Drummond J. D. (1981). “A test of comet and meteor shower associations”. Icarus, 45, 545–553.
Hawkins G. S. (1963). “The Harvard radio meteor project”. Smithsonian Contributions to Astrophysics, 7, 53–62.
Jenniskens P., Gural P. S., Grigsby B., Dynneson L., Koop M. and Holman D. (2011). “CAMS: Cameras for Allsky Meteor Surveillance to validate minor meteor showers”. Icarus, 216, 40–61.
Jenniskens P. and Haberman B. (2013). “Thatcher’s Ghost: Confirmation of the Nu Cygnids (NCY, IAU#409)”. WGN, Journal of the International Meteor Organization, 41, 75–76
Jenniskens P., Nénon Q., Albers J., Gural P. S., Haberman B., Holman D., Morales R., Grigsby B. J., Samuels D. and Johannink C. (2016). “The established meteor showers as observed by CAMS”. Icarus, 266, 331–354.
Jenniskens P., Baggaley J., Crumpton I., Aldous P., Pokorny P., Janches D., Gural P. S., Samuels D., Albers J., Howell A., Johannink C., Breukers M., Odeh M., Moskovitz N., Collison J. and Ganjuag S. (2018). “A survey of southern hemisphere meteor showers”. Planetary Space Science, 154, 21–29.
Jopek T. J. (1993). “Remarks on the meteor orbital similarity D-criterion”. Icarus, 106, 603–607.
Kornoš L., Matlovič P., Rudawska R., Tóth J., Hajduková M. Jr., Koukal J. and Piffl R. (2014). “Confirmation and characterization of IAU temporary meteor showers in EDMOND database”. In Jopek T. J., Rietmeijer F. J. M., Watanabe J., Williams I. P., editors, Proceedings of the Meteoroids 2013 Conference, Poznań, Poland, Aug. 26-30, 2013. A.M. University, pages 225–233.
Molau S. and Rendtel J. (2009). “A comprehensive list of meteor showers obtained from 10 years of observations with the IMO Video Meteor Network”. WGN, Journal of the International Meteor Organization, 37, 98–121.
Phillips M., Jenniskens P. and Grigsby B. (2011). “Confirmation of the April Rho Cygnids (ARC, IAU#348)”. WGN, Journal of the International Meteor Organization, 39, 131–136.
Roggemans P. (2018). “August gamma Cepheids (523-AGC)”. eMetN, 3, 73–78.
Roggemans P. and Cambell-Burns P. (2018a). “x Herculids (XHE-346)”. eMetN, 3, 120–127.
Roggemans P. and Cambell-Burns P. (2018b). “February Hydrids (FHY-1032)”. eMetN, 3, 128–133.
Roggemans P. and Cambell-Burns P. (2018c). “Alpha Aquariids (AAQ-927)”. eMetN, 3, 134–141.
Roggemans P. and Cambell-Burns P. (2018d). “Eta Lyrids (ELY-145)”. eMetN, 3, 142–147.
Roggemans P. and Johannink C. (2018). “A search for December alpha Bootids (497)”. eMetN, 3, 64–72.
Sekanina Z. (1976). “Statistical model of meteor streams. IV – A study of radio streams from the synoptic year.” Icarus, 27, 265–321.
SonotaCo (2009). “A meteor shower catalog based on video observations in 2007-2008”. WGN, Journal of the International Meteor Organization, 37, 55–62.
Southworth R. R. and Hawkins G. S. (1963). “Statistics of meteor streams”. Smithson. Contrib. Astrophys., 7, 261–286.